8 changed files with 295 additions and 0 deletions
Unified View
Diff Options
-
BINDergunPiotr-WaskoDominik/zad3/macierz_gpu
-
+5 -0DergunPiotr-WaskoDominik/zad4/Makefile
-
+40 -0DergunPiotr-WaskoDominik/zad4/Ttiming.h
-
BINDergunPiotr-WaskoDominik/zad4/dane/czas.jpg
-
BINDergunPiotr-WaskoDominik/zad4/dane/przyspieszenie.jpg
-
+19 -0DergunPiotr-WaskoDominik/zad4/dane/wykres.gnuplot
-
+117 -0DergunPiotr-WaskoDominik/zad4/dok.tex
-
+114 -0DergunPiotr-WaskoDominik/zad4/gauss_omp.cpp
BIN
DergunPiotr-WaskoDominik/zad3/macierz_gpu
View File
+ 5
- 0
DergunPiotr-WaskoDominik/zad4/Makefile
View File
| @ -0,0 +1,5 @@ | |||||
| macierz_omp: gauss_omp.cpp | |||||
| g++ -O3 -fopenmp -Wall `pkg-config opencv --cflags --libs` -o gauss_omp gauss_omp.cpp | |||||
| clean: | |||||
| rm -rf gauss_omp | |||||
+ 40
- 0
DergunPiotr-WaskoDominik/zad4/Ttiming.h
View File
| @ -0,0 +1,40 @@ | |||||
| #if !defined(DEF_TTIMING) | |||||
| #define DEF_TTIMING | |||||
| #include <sys/time.h> | |||||
| class TTiming | |||||
| { | |||||
| protected: | |||||
| struct timeval start; | |||||
| struct timeval stop; | |||||
| void getTime(timeval &tv); | |||||
| public: | |||||
| TTiming(void); | |||||
| void Begin(void); | |||||
| long End(void); | |||||
| }; | |||||
| inline TTiming::TTiming(void) | |||||
| { | |||||
| } | |||||
| inline void TTiming::Begin(void) | |||||
| { | |||||
| getTime(start); | |||||
| } | |||||
| inline long TTiming::End(void) | |||||
| { | |||||
| getTime(stop); | |||||
| return ((stop.tv_sec-start.tv_sec) * 1000 + (stop.tv_usec-start.tv_usec)/1000.0) + 0.5; | |||||
| } | |||||
| inline void TTiming::getTime(timeval &tv) | |||||
| { | |||||
| gettimeofday(&tv,NULL); | |||||
| } | |||||
| #endif | |||||
BIN
DergunPiotr-WaskoDominik/zad4/dane/czas.jpg
View File
BIN
DergunPiotr-WaskoDominik/zad4/dane/przyspieszenie.jpg
View File
+ 19
- 0
DergunPiotr-WaskoDominik/zad4/dane/wykres.gnuplot
View File
| @ -0,0 +1,19 @@ | |||||
| #set terminal x11 | |||||
| set terminal jpeg | |||||
| set xrange [0:16] | |||||
| set yrange [0:6] | |||||
| set xlabel "Liczba watkow [n]" | |||||
| set ylabel "Przyspieszenie [n]" | |||||
| set out "przyspieszenie.jpg" | |||||
| plot \ | |||||
| "wyniki.txt" using 1:3 with points ls 3 lc rgb "red" title "przyspieszenie", \ | |||||
| "wyniki.txt" using 1:3 with lines ls 3 lc rgb "blue" notitle | |||||
| set out "czas.jpg" | |||||
| set ylabel "Czas obliczen [ms]" | |||||
| set yrange [0:16000] | |||||
| plot \ | |||||
| "wyniki.txt" using 1:2 with points ls 3 lc rgb "red" title "czas", \ | |||||
| "wyniki.txt" using 1:2 with lines ls 3 lc rgb "blue" notitle | |||||
+ 117
- 0
DergunPiotr-WaskoDominik/zad4/dok.tex
View File
| @ -0,0 +1,117 @@ | |||||
| \documentclass[a4paper,12pt]{article} | |||||
| \usepackage{amsmath} | |||||
| \usepackage{amssymb} | |||||
| \usepackage[polish]{babel} | |||||
| \usepackage{polski} | |||||
| \usepackage[utf8]{inputenc} | |||||
| \usepackage{indentfirst} | |||||
| \usepackage{geometry} | |||||
| \usepackage{array} | |||||
| \usepackage[pdftex]{color,graphicx} | |||||
| \usepackage{subfigure} | |||||
| \usepackage{afterpage} | |||||
| \usepackage{setspace} | |||||
| \usepackage{color} | |||||
| \usepackage{wrapfig} | |||||
| \usepackage{listings} | |||||
| \usepackage{datetime} | |||||
| \renewcommand{\onehalfspacing}{\setstretch{1.6}} | |||||
| \geometry{tmargin=2.5cm,bmargin=2.5cm,lmargin=2.5cm,rmargin=2.5cm} | |||||
| \setlength{\parindent}{1cm} | |||||
| \setlength{\parskip}{0mm} | |||||
| \newenvironment{lista}{ | |||||
| \begin{itemize} | |||||
| \setlength{\itemsep}{1pt} | |||||
| \setlength{\parskip}{0pt} | |||||
| \setlength{\parsep}{0pt} | |||||
| }{\end{itemize}} | |||||
| \newcommand{\linia}{\rule{\linewidth}{0.4mm}} | |||||
| \definecolor{lbcolor}{rgb}{0.95,0.95,0.95} | |||||
| \lstset{ | |||||
| backgroundcolor=\color{lbcolor}, | |||||
| tabsize=4, | |||||
| language=C++, | |||||
| captionpos=b, | |||||
| tabsize=3, | |||||
| frame=lines, | |||||
| numbers=left, | |||||
| numberstyle=\tiny, | |||||
| numbersep=5pt, | |||||
| breaklines=true, | |||||
| showstringspaces=false, | |||||
| basicstyle=\footnotesize, | |||||
| identifierstyle=\color{magenta}, | |||||
| keywordstyle=\color[rgb]{0,0,1}, | |||||
| commentstyle=\color{Darkgreen}, | |||||
| stringstyle=\color{red} | |||||
| } | |||||
| \begin{document} | |||||
| \noindent | |||||
| \begin{tabular}{|c|p{11cm}|c|} \hline | |||||
| Grupa 1 & Piotr Dergun, Dominik Waśko & \ddmmyyyydate\today \tabularnewline | |||||
| \hline | |||||
| \end{tabular} | |||||
| \section*{Zadanie 1 - Macierze OMP} | |||||
| Celem zadania jest obliczenie iloczynu dwóch macierzy prostokątnych na konkretnej liczbie wątków (dane te podane jako parametry programu). Istotą problemu są trzy pętle, których złożoność obliczeniowa jest O($n^3$) | |||||
| \begin{lstlisting} | |||||
| #pragma omp parallel for default(none) shared(A, B, C) firstprivate(rozmiar)private(i, j) | |||||
| for (i=0; i<rozmiar; ++i) | |||||
| for (j=0; j<rozmiar; ++j) | |||||
| { | |||||
| C[i][j] = 0; | |||||
| for (long k=0; k<rozmiar; ++k) | |||||
| C[i][j] += A[i][k]*B[k][j]; | |||||
| } | |||||
| \end{lstlisting} | |||||
| Zmienna \textit{i} ma za zadanie przechodzić po wierszach macierzy wyjściowej, a zmienna \textit{j} - jej kolumnach. Za przemnażanie wszystkich elementów z wektora macierzy A (po wierszach) i wektora macierzy B (po kolumnach) odpowiedzialna jest wewnętrzna pętla. | |||||
| Poniższa dyrektywa: | |||||
| \begin{lstlisting} | |||||
| #pragma omp parallel for default(shared) | |||||
| \end{lstlisting} | |||||
| oznacza, że wszystkie zmienne w przetwarzanym równolegle bloku kodu będą zmiennymi współdzielonymi, z wyjątkiem liczników pętli | |||||
| Natomiast dyrektywa | |||||
| \begin{lstlisting} | |||||
| #pragma omp parallel for default(none) shared(A, B, C) | |||||
| firstprivate(rozmiar)private(i, j) | |||||
| \end{lstlisting} | |||||
| oznacza, że współdzielone będą wskaźniki tablic (A,C,B), zmienna \textit{rozmiar} jest prywatna dla każdego wątki i gdy jest tworzona jest kopią zmiennej globalnej. Zmienne \textit{i} i \textit{j} są prywatne. | |||||
| Program został skompilowany i uruchomiony z następującymi parametrami: macierz 1500x1500, ilość wątków 1-15, dla każdego wątku wykonano 10 powtórzeń. Z otrzymanych wyników obliczono przyspieszenie oraz średni czas liczenia macierzy. | |||||
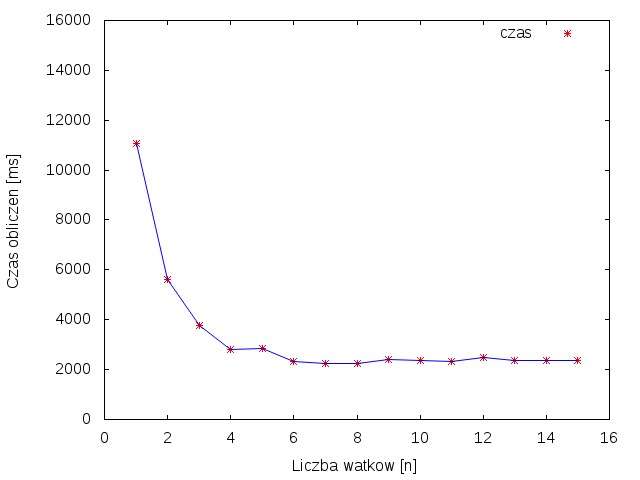
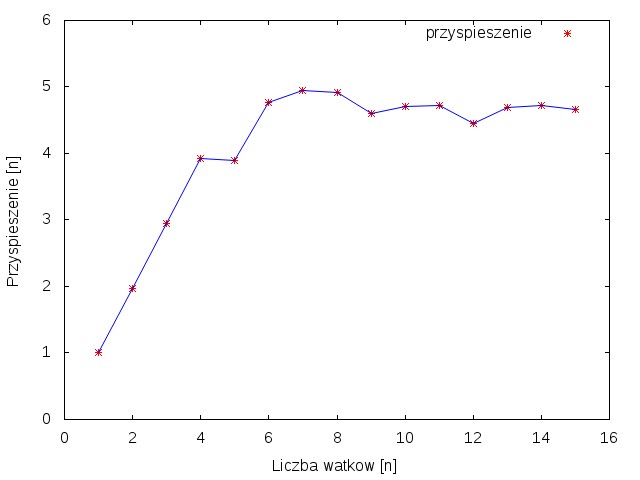
| Rysunek 1 przedstawia wykres zależności przyspieszenia od ilości wątków. Można na nim zauważać że wzrost przyspieszenia uzyskuje się tylko do momentu gdy liczba wątków jest mniejsza lub równa 4. Spowodowane jest to tym, że komputer na którym obliczane było zadanie posiada procesor o 4 rdzeniach oraz wykorzystuje technologię HyperThreading która pozwala na prace w sumie ośmiu wątków. Rysunek 2. przedstawia wykres zależności czasu obliczeń od liczby wątków. Można zobaczyć na nim, że powyżej 4 wątków czas obliczeń nie ulega już skróceniu. | |||||
| Z powyższych obserwacji wynika, że wykorzystanie większej liczby wątków pozwala znacząco skrócić czas wykonania programu. Jednak zwiększanie liczby wątków ponad to co oferuje procesor nie powoduje wzrostu wydajności i wymusza współbieżne liczenie. | |||||
| \begin{figure}[!h] | |||||
| \centering | |||||
| \includegraphics[width=0.7\textwidth]{dane/przyspieszenie.jpg} | |||||
| \caption{Wykres zależności przyspieszenia obliczeń od liczby wykorzystanych wątków} | |||||
| \end{figure} | |||||
| \begin{figure}[!h] | |||||
| \centering | |||||
| \includegraphics[width=0.7\textwidth]{dane/czas.jpg} | |||||
| \caption{Wykres zależności czasu obliczeń od liczby wykorzystanych wątków} | |||||
| \end{figure} | |||||
| \end{document} | |||||
+ 114
- 0
DergunPiotr-WaskoDominik/zad4/gauss_omp.cpp
View File
| @ -0,0 +1,114 @@ | |||||
| #include <iostream> | |||||
| #include <cstdlib> | |||||
| #include <cmath> | |||||
| #include <omp.h> | |||||
| #include "Ttiming.h" | |||||
| #include <opencv2/opencv.hpp> | |||||
| using namespace std; | |||||
| using namespace cv; | |||||
| #define RX 5 | |||||
| #define RY 5 | |||||
| int main(int argc, char *argv[]) | |||||
| { | |||||
| int i,j,k,l,m,n; | |||||
| TTiming tt; | |||||
| char *endptr; | |||||
| int ratio[RX][RY] = | |||||
| { | |||||
| {1, 4, 7, 4, 1}, | |||||
| {4, 16, 26, 16, 4}, | |||||
| {7, 26, 41, 26, 7}, | |||||
| {4, 16, 26, 16, 4}, | |||||
| {1, 4, 7, 4, 1} | |||||
| }; | |||||
| if (argc < 4) | |||||
| { | |||||
| cerr << "Usage: " << argv[0] << " <n> <input_image> <output_image>" << endl; | |||||
| exit(1); | |||||
| } | |||||
| int threads_num = strtol(argv[1], &endptr, 10); | |||||
| if (*endptr) | |||||
| { | |||||
| cerr << "Invalid number of threads format" << endl; | |||||
| exit(1); | |||||
| } | |||||
| if (threads_num <= 0) | |||||
| { | |||||
| cerr << "The number of threads must be positive" << endl; | |||||
| exit(1); | |||||
| } | |||||
| int suma_wag = 0; | |||||
| for (i=0; i<RX; ++i) | |||||
| for (j=0; j<RY; ++j) | |||||
| suma_wag += ratio[i][j]; | |||||
| //ustawienie odpowiedniej ilosci watkow | |||||
| omp_set_num_threads(threads_num); | |||||
| Mat img = cv::imread(argv[2]); | |||||
| if(!img.data ) | |||||
| { | |||||
| cerr << "File " << argv[2] << " does not exist" << endl; | |||||
| exit(1); | |||||
| } | |||||
| Mat img_out; | |||||
| img_out.create(img.rows, img.cols, img.type()); | |||||
| int sumka_r, sumka_g, sumka_b; | |||||
| //#pragma omp parallel for default(shared) | |||||
| tt.Begin(); | |||||
| //#pragma omp parallel for default(shared) | |||||
| #pragma omp parallel for private(i, j, k, l, m, n, sumka_r, sumka_g, sumka_b) | |||||
| for (i=0; i<img.rows; ++i) | |||||
| { | |||||
| for (j=0; j<img.cols; ++j) | |||||
| { | |||||
| if (i<2 || i>img.rows-3 || j<2 || j>img.cols-3) | |||||
| { | |||||
| img_out.at<Vec3b>(i, j)[0] = img.at<Vec3b>(i, j)[0]; | |||||
| img_out.at<Vec3b>(i, j)[1] = img.at<Vec3b>(i, j)[1]; | |||||
| img_out.at<Vec3b>(i, j)[2] = img.at<Vec3b>(i, j)[2]; | |||||
| } | |||||
| else | |||||
| { | |||||
| sumka_r = 0; | |||||
| sumka_g = 0; | |||||
| sumka_b = 0; | |||||
| m=i-2; | |||||
| for (k=0; k<RX; ++k,++m) | |||||
| { | |||||
| n=j-2; | |||||
| for (l=0; l<RY; ++l,++n) | |||||
| { | |||||
| sumka_b += ratio[k][l] * img.at<Vec3b>(m, n)[0]; | |||||
| sumka_g += ratio[k][l] * img.at<Vec3b>(m, n)[1]; | |||||
| sumka_r += ratio[k][l] * img.at<Vec3b>(m, n)[2]; | |||||
| } | |||||
| } | |||||
| img_out.at<Vec3b>(i, j).val[0] = sumka_b / suma_wag; | |||||
| img_out.at<Vec3b>(i, j).val[1] = sumka_g / suma_wag; | |||||
| img_out.at<Vec3b>(i, j).val[2] = sumka_r / suma_wag; | |||||
| } | |||||
| //cout << img_out.at<Vec3b>(i, j)[0].val[0]; | |||||
| } | |||||
| } | |||||
| long elapsed = tt.End(); | |||||
| cout << "Time: " << elapsed << " ms" << endl; | |||||
| imwrite(argv[3], img_out); | |||||
| exit(0); | |||||
| } | |||||