INIT: zad5 (dziala)

DergunPiotr-WaskoDominik/zad4/Makefile

@@ -1,4 +1,4 @@
-macierz_omp: gauss_omp.cpp
+gauss_omp: gauss_omp.cpp
 	g++ -O3 -fopenmp -Wall -o gauss_omp gauss_omp.cpp `pkg-config opencv --cflags --libs`
 
 clean:

DergunPiotr-WaskoDominik/zad5/Makefile

@@ -0,0 +1,5 @@
+gauss_mpi: gauss_mpi.cpp
+	mpicxx -Wall -o gauss_mpi gauss_mpi.cpp `pkg-config opencv --cflags --libs`
+
+clean:
+	rm -rf gauss_mpi

DergunPiotr-WaskoDominik/zad5/Ttiming.h

@@ -0,0 +1,40 @@
+#if !defined(DEF_TTIMING)
+#define DEF_TTIMING
+#include <sys/time.h>
+
+class TTiming
+{
+protected:
+	struct timeval start;
+	struct timeval stop;
+	void getTime(timeval &tv);
+	
+public:
+	TTiming(void);
+
+	void Begin(void);
+	long End(void);
+};
+
+inline TTiming::TTiming(void)
+{
+
+}
+
+inline void TTiming::Begin(void)
+{
+	getTime(start);
+}
+
+inline long TTiming::End(void)
+{
+	getTime(stop);
+	return ((stop.tv_sec-start.tv_sec) * 1000 + (stop.tv_usec-start.tv_usec)/1000.0) + 0.5;
+}
+
+inline void TTiming::getTime(timeval &tv)
+{
+	gettimeofday(&tv,NULL);
+}
+
+#endif

DergunPiotr-WaskoDominik/zad5/dane/wykres.gnuplot

@@ -0,0 +1,19 @@
+#set terminal x11
+set terminal jpeg
+set xrange [0:16]
+set yrange [0:7]
+
+set xlabel "Liczba watkow [n]"
+set ylabel "Przyspieszenie [n]"
+
+set out "przyspieszenie.jpg"
+plot \
+ "wyniki.txt" using 1:3 with points ls 3 lc rgb "red" title "przyspieszenie", \
+ "wyniki.txt" using 1:3 with lines ls 3 lc rgb "blue" notitle
+
+set out "czas.jpg"
+set ylabel "Czas obliczen [ms]"
+set yrange [0:16000]
+plot \
+ "wyniki.txt" using 1:2 with points ls 3 lc rgb "red" title "czas", \
+ "wyniki.txt" using 1:2 with lines ls 3 lc rgb "blue" notitle

DergunPiotr-WaskoDominik/zad5/dane/wyniki.txt

@@ -0,0 +1,15 @@
+1	13230	1.0
+2	6706	1.9729
+3	4462	2.965
+4	3344	3.9563
+5	2690	4.9182
+6	2271	5.8256
+7	2689	4.92
+8	2529	5.2313
+9	2459	5.3802
+10	2358	5.6107
+11	2348	5.6346
+12	2257	5.8618
+13	2351	5.6274
+14	2327	5.6854
+15	2310	5.7273

DergunPiotr-WaskoDominik/zad5/dok.tex

@@ -0,0 +1,127 @@
+\documentclass[a4paper,12pt]{article}
+\usepackage{amsmath}
+\usepackage{amssymb}
+\usepackage[polish]{babel}
+\usepackage{polski}
+\usepackage[utf8]{inputenc}
+\usepackage{indentfirst}
+\usepackage{geometry}
+\usepackage{array}
+\usepackage[pdftex]{color,graphicx}
+\usepackage{subfigure}
+\usepackage{afterpage}
+\usepackage{setspace}
+\usepackage{color}
+\usepackage{wrapfig}
+\usepackage{listings}
+\usepackage{datetime}
+
+\renewcommand{\onehalfspacing}{\setstretch{1.6}}
+
+\geometry{tmargin=2.5cm,bmargin=2.5cm,lmargin=2.5cm,rmargin=2.5cm}
+\setlength{\parindent}{1cm}
+\setlength{\parskip}{0mm}
+
+\newenvironment{lista}{
+\begin{itemize}
+  \setlength{\itemsep}{1pt}
+  \setlength{\parskip}{0pt}
+  \setlength{\parsep}{0pt}
+}{\end{itemize}}
+
+\newcommand{\linia}{\rule{\linewidth}{0.4mm}}
+
+\definecolor{lbcolor}{rgb}{0.95,0.95,0.95}
+\lstset{
+    backgroundcolor=\color{lbcolor},
+    tabsize=4,
+  language=C++,
+  captionpos=b,
+  tabsize=3,
+  frame=lines,
+  numbers=left,
+  numberstyle=\tiny,
+  numbersep=5pt,
+  breaklines=true,
+  showstringspaces=false,
+  basicstyle=\footnotesize,
+  identifierstyle=\color{magenta},
+  keywordstyle=\color[rgb]{0,0,1},
+  commentstyle=\color{Darkgreen},
+  stringstyle=\color{red}
+  }
+
+\begin{document}
+
+\noindent
+\begin{tabular}{|c|p{11cm}|c|} \hline 
+Grupa 1 & Piotr Dergun, Dominik Waśko & \ddmmyyyydate\today \tabularnewline
+\hline 
+\end{tabular}
+
+
+\section*{Zadanie 4 - Rozmycie Gaussa w OpenMP}
+
+Celem zadania jest wykonanie rozmycia obrazu za pomocą algorytmu  Gaussa o rozmiarze maski 5x5
+
+\begin{lstlisting}
+	#pragma omp parallel for private(i, j, k, l, m, n, sumka_r, sumka_g, sumka_b)
+	for (i=0; i<img.rows; ++i){
+		for (j=0; j<img.cols; ++j){
+			if (i<2 || i>img.rows-3 || j<2 || j>img.cols-3){
+				img_out.at<Vec3b>(i, j)[0] = img.at<Vec3b>(i, j)[0];
+				img_out.at<Vec3b>(i, j)[1] = img.at<Vec3b>(i, j)[1];
+				img_out.at<Vec3b>(i, j)[2] = img.at<Vec3b>(i, j)[2];
+			}
+			else{
+				sumka_r = 0;
+				sumka_g = 0;
+				sumka_b = 0;
+				m=i-2;
+				for (k=0; k<RX; ++k,++m){
+					n=j-2;
+					for (l=0; l<RY; ++l,++n){
+						sumka_b += ratio[k][l] * img.at<Vec3b>(m, n)[0]; 
+						sumka_g += ratio[k][l] * img.at<Vec3b>(m, n)[1]; 
+						sumka_r += ratio[k][l] * img.at<Vec3b>(m, n)[2]; 
+					}	
+				}
+				img_out.at<Vec3b>(i, j).val[0] = sumka_b / suma_wag;
+				img_out.at<Vec3b>(i, j).val[1] = sumka_g / suma_wag;
+				img_out.at<Vec3b>(i, j).val[2] = sumka_r / suma_wag;
+			}
+		}
+	}
+\end{lstlisting}
+
+Zmienne \textit{i} oraz \textit{j}  służą do iteracji po wszystkich  pikselach obrazu. W przypadkach brzegowych tzn. 2 piksele od krawędzi obrazu,  piksele są pozostawiane bez zmian. Jest to spowodowane tym, że w przypadku tych pikseli nie można zastosować maski 5x5. Wartość pozostałych pikseli jest zmieniana przy pomocy algorytmu Gaussa.
+
+Do wczytania obrazu użyto biblioteki OpenCV. 
+
+Zadanie zostało uruchomione na komputerze  MacPro3,1 wyposażonym w  2 procesory Xeon E5462, przy czym do dyspozycji było 6 rdzeni.  
+
+Program został uruchomiony dla obrazu o rozmiarze AxB. Obliczenia przeprowadzono tworząc od 1 do 15 wątków, dla każdej ilości wykonano 10 powtórzeń. Z otrzymanych wyników obliczono przyspieszenie oraz średni czas obliczania rozmycia. 
+
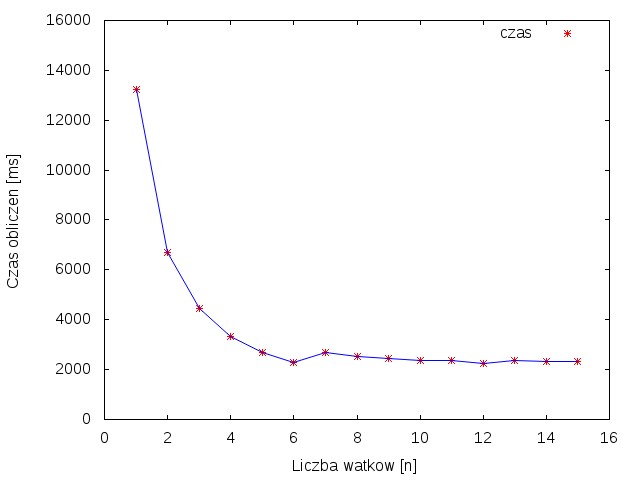
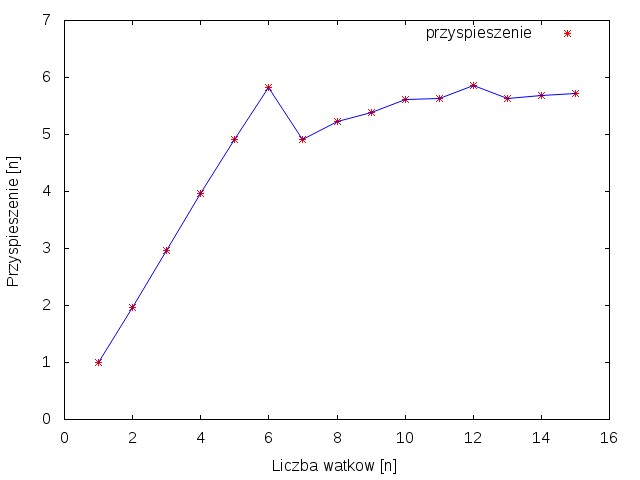
+Rysunek 1 przedstawia wykres zależności przyspieszenia od ilości wątków. Można na nim zauważać że wzrost przyspieszenia uzyskuje się tylko do momentu gdy liczba wątków jest mniejsza lub równa ilości rdzeni. Powyżej sześciu następuje już przetwarzanie współbieżne. Rysunek 2. przedstawia wykres zależności czasu obliczeń od liczby wątków.  Można zobaczyć na nim, że powyżej 6 wątków czas obliczeń nie ulega już skróceniu. 
+
+Z powyższych obserwacji wynika, że wykorzystanie większej liczby wątków pozwala znacząco skrócić czas wykonania programu. Jednak zwiększanie liczby wątków ponad to co oferuje procesor nie powoduje wzrostu wydajności i wymusza współbieżne liczenie.
+
+
+
+
+\begin{figure}[!h]
+	\centering
+  \includegraphics[width=0.7\textwidth]{dane/przyspieszenie.jpg}
+  \caption{Wykres zależności przyspieszenia obliczeń od liczby wykorzystanych wątków}
+\end{figure}
+
+
+\begin{figure}[!h]
+	\centering
+  \includegraphics[width=0.7\textwidth]{dane/czas.jpg}
+  \caption{Wykres zależności czasu obliczeń od liczby wykorzystanych wątków}
+\end{figure}
+
+
+
+\end{document}

DergunPiotr-WaskoDominik/zad5/gauss_mpi.cpp

@@ -0,0 +1,150 @@
+#include <iostream>
+#include <cstdlib>
+#include <cmath>
+#include <mpi.h>
+#include "Ttiming.h"
+#include <opencv2/opencv.hpp>
+
+using namespace std;
+using namespace cv;
+
+#define RX 5
+#define RY 5
+int main(int argc, char *argv[])
+{
+	int i,j,k,l,m,n;
+	TTiming tt;
+	int sumka_r, sumka_g, sumka_b;
+	int suma_wag = 0;
+	Mat img_out;
+	int buff_max=0,porcja_new=0;
+	Mat img;
+	Mat img_part_out;
+
+	int ratio[RX][RY] =
+	{
+		{1, 4, 7, 4, 1},
+		{4, 16, 26, 16, 4},
+		{7, 26, 41, 26, 7},
+		{4, 16, 26, 16, 4},
+		{1, 4, 7, 4, 1}
+	};
+	
+	if (argc < 3)
+	{
+		cerr << "Usage: " << argv[0] << " <input_image> <output_image>" << endl;
+		exit(1);
+	}
+
+	img = cv::imread(argv[1]);
+	if(!img.data )
+	{
+		cerr << "File " << argv[1] << " does not exist" << endl;
+		MPI::Finalize();
+		exit(1);
+	}
+	
+	for (i=0; i<RX; ++i)
+		for (j=0; j<RY; ++j)
+			suma_wag += ratio[i][j];
+	
+	MPI::Init(argc, argv);
+
+	int taskid = MPI::COMM_WORLD.Get_rank();
+	int ntasks = MPI::COMM_WORLD.Get_size();
+	
+	// porcja - ile wektorów dostaje jeden proces do liczenia
+	// jeżeli liczba procesów większa od wektorów - każdy proces dostaje po jednym, niektóre wcale
+	int porcja = (img.rows>=ntasks) ? (int)round(img.rows*1.0/ntasks) : 1;
+	//porcja *= img.cols; //porcję mnożymy przez ilość elementów w jednym wektorze
+	porcja_new = porcja;
+
+	// dla kompatybilności liczę jeszcze rozmiar bufora odbioru,
+	// np. jeżeli chunki będą jednolitego rozmiaru, a ostatni będzie większy
+	// to bufor odbioru musi być zwiększony (żeby go nie ucinało)
+	buff_max = img.rows - porcja*(ntasks-1);
+	if (porcja > buff_max)
+		buff_max = porcja; // na wypadek, jeżeli jednak ostatni kawałek będzie mniejszy 
+	
+	if (taskid == 0)
+		img_out.create(/*buff_max*ntasks*/img.rows, img.cols, img.type());
+		
+	MPI::COMM_WORLD.Barrier();
+
+	//
+	// część licząca ---------------------------------------------------------------------------------
+	//
+	
+	MPI::COMM_WORLD.Barrier();
+	if (taskid == 0)
+		tt.Begin();
+	int start_pos = taskid*porcja;
+	int stop_pos = (taskid+1)*porcja;
+
+	if (taskid == ntasks -1) //przelicz porcję dla ostatniego procesu (w przypadku dzielenia z resztą)
+	{
+		porcja_new = img.rows - porcja*(ntasks-1);
+		
+		// myk jest taki, że muszę podać jakąś niezerową porcję do gathera,
+		// mimo, że proces nie ma żadnych (sensownych) danych do przetworzenia
+		if (porcja_new > 0)
+		{
+			stop_pos = img.rows;
+			porcja = porcja_new;
+		}
+	}
+	img_part_out.create(porcja, img.cols, img.type());
+
+	int p=0, q=0;
+
+	for (i=start_pos; i<stop_pos; ++i)
+	{
+		q = 0;
+		for (j=0; j<img.cols; ++j)
+		{
+			if (i<2 || i>img.rows-3 || j<2 || j>img.cols-3)
+			{
+				img_part_out.at<Vec3b>(p, q)[0] = img.at<Vec3b>(i, j)[0];
+				img_part_out.at<Vec3b>(p, q)[1] = img.at<Vec3b>(i, j)[1];
+				img_part_out.at<Vec3b>(p, q)[2] = img.at<Vec3b>(i, j)[2];
+			}
+			else
+			{
+				sumka_r = 0;
+				sumka_g = 0;
+				sumka_b = 0;
+				m=i-2;
+				for (k=0; k<RX; ++k,++m)
+				{
+					n=j-2;
+					for (l=0; l<RY; ++l,++n)
+					{
+						sumka_b += ratio[k][l] * img.at<Vec3b>(m, n)[0]; 
+						sumka_g += ratio[k][l] * img.at<Vec3b>(m, n)[1]; 
+						sumka_r += ratio[k][l] * img.at<Vec3b>(m, n)[2]; 
+					}	
+				}
+				img_part_out.at<Vec3b>(p, q).val[0] = sumka_b / suma_wag;
+				img_part_out.at<Vec3b>(p, q).val[1] = sumka_g / suma_wag;
+				img_part_out.at<Vec3b>(p, q).val[2] = sumka_r / suma_wag;
+			}
+			++q;
+		}
+		++p;
+	}
+
+	MPI::COMM_WORLD.Barrier();
+	if (taskid == 0)
+	{
+		long elapsed = tt.End();	
+		cout << "Time: " << elapsed << " ms" << endl;
+	}
+	// zwróć wszystko do programu głównego
+	MPI::COMM_WORLD.Gather(&img_part_out.data[0], porcja*img.cols*3, MPI::CHAR, &img_out.data[0], porcja*img.cols*3, MPI::CHAR, 0);
+
+	if (taskid == 0)
+		imwrite(argv[2], img_out);
+	MPI::Finalize();
+
+	exit(0);
+}